
Die Kraft, die den Bolzen beschleunigt, entspricht den Rückstellkräften der als Blattfedern wirkenden Halbarme des Bogens. Die Sehne wird zunächst als absolut nicht-elastisch angenommen. Dies ist nur ein vereinfachtes Rechenmodell. Zu beachten ist bei einer realen Armbrust zusätzlich eine evtl. Vorspannung der Arme und eine Elastizität der Sehne. Bei einem Bogen aus Holz ist der entsprechende E-Modul des Holzes zu verwenden. Man beachte, dass es sich bei Holz um einen anisotropen Werkstoff handelt (Faserrichtung beachten).
Nehmen wir die Arme der Armbrust einfach als mittig und senkrecht belasteten Biegebalken an. Genaugenommen handelt es sich um zwei fest eingespannte Träger aber das ist in diesem Fall äquivalent zu einem statisch bestimmt gelagerten Biegebalken (siehe Skizze 1). In einem Buch über Technische Mechanik finden wir die Formel für maximale Durchbiegung (Gleichung 1):


mit:
F: Kraft
l: Länge des unbelasteten (!) Trägers
E: E-Modul
J: Flächenträgheitsmoment
Die aufgebrachte Kraft ist bei gegebener Durchbiegung abhängig vom Werkstoff (E-Modul) und der Geometrie (Flächenträgheitsmoment und Länge) des Balkens.
Das Flächenträgheitsmoment des Bogens wird über die Bogenlänge als konstant angenommen, d.h. der Querschnitt ändert sich nicht. Für Achse 2 berechnet sich das FTM dann gemäß Gleichung 2:


Die Auszuglänge s und der Spannwinkel α richten sich nach der maximal zulässigen Seilkraft der Sehne und der gewünschten Baulänge. Die Auszuglänge s lässt sich Skizze 3 entnehmen.

Ist die Durchbiegung w klein, gilt Gleichung 3, da die Längenänderung des Balkens vernachlässigt werden kann. Gesucht ist die Höhe k des gleichschenkligen Dreiecks, das von der Sehne aufgespannt wird.

und damit

Die Seilkraft Fs lässt sich aus Skizze 4 ablesen. Sie entsteht durch Vektorzerlegung der Gesamtkraft in die einzelnen Seilkräfte der Halbarme.

Sie berechnet sich nach Gleichung 4 zu:

Berechnung der Durchbiegung bei gegebener Last anhand einer schweren Armbrust mit Stahl-Armen und einer nicht-elatischen Sehne.
Gegeben:
F = 500 N (entspricht ca. 50 kg)
E = 210.000 N/mm² (E-Modul von Stahl)
l = 600 mm
b = 5 mm
h = 20 mm
α = 30°
Gesucht:
wmax = ?
Rechnung:

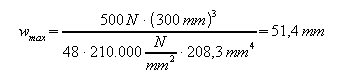


Kleinere Armbrüste haben einen feststehenden Bogen, an dem ein Gummiseil befestigt ist. Die Kraft entsteht durch die Rückstellkraft des gedehnten Gummiseils. Die folgende Tabelle und das Diagramm zeigen die gemessenen Werte für eine selbstgebaute Armbrust:
| Auszug [mm] | Gewicht [g] | Zugkraft [lbs] |
| 0 | 0 | 0 |
| 20 | 800 | 1,76 |
| 30 | 1300 | 2,86 |
| 45 | 1800 | 3,96 |
| 60 | 2300 | 5,06 |
| 70 | 2800 | 6,16 |
| 85 | 3300 | 7,26 |
| 110 | 4300 | 9,46 |
| 135 | 5000 | 11 |
| 150 | 5500 | 12,1 |
| 160 | 6500 | 14,3 |
| 180 | 7500 | 16,5 |
| 205 | 8500 | 18,7 |
| 225 | 9500 | 20,9 |
| 240 | 10500 | 23,1 |
| 260 | 11500 | 25,3 |
| max. 260 mm | max. 11,5 kg | |
| 10 inch | 25 lbs | Energie: 15 J |
Wie die Werte und das Diagramm (zum Vergrößern bitte anklicken) zeigen, verhält sich der Expander annähernd linear-elastisch. Zu beachten sind Messfehler (Ablesefehler bei Gewicht und Strecke), aber die Linearität darf angenommen werden.
Da es sich um ein linear-elastisches Gummiseil handelt, berechnet sich die Rückstellkraft - genau wie bei einer Feder - nach dem Hook'schen Gesetz (Gl. 5). Dies ist genau die Kraft, die man aufbringen muss, um zum Beispiel einen Expander (daraus werden viele Sehnen von LARP-Armbrüsten gebaut) auseinander zu ziehen. Die Rückstellkraft ist dabei proportional zur Auszuglänge, der Proportionalitätsfaktor ist die Federsteifigkeit. Die Rückstellkraft entspricht genau der Seilkraft.

mit:
Frück: Rückstellkraft
cF: Federsteifigkeit (Materialkennwert)
s: Federweg
Zur Berechnung der benötigten Auszugslänge k bei einer Kraft F < Fzul (mit Fzul, LARP = 150 N) ziehen wir wieder Skizze 3 heran und treffen folgende Annahmen:

Gesucht ist die Länge der Sehne im gespannten Zustand, um die Rückstellkraft bzw. Seilkraft (es gilt Frück = Fs) nach Gl. 5 zu berechnen. Gesucht ist also die Summe der zwei Hypothenusen c. Die Hypothenuse c lässt sich entweder unter Vorgabe der Sehnenlänge l und des Sehnenwinkels α oder der Sehnenlänge l und der Auszuglänge k bestimmen (Gl. 6a/6b).

Der Federweg s berechnet sich damit zu
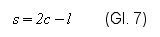
Mit dem Federweg s kann die Seilkraft Fs im gespannten Zustand (entspricht Fs,max) mit Hilfe von Gl. 5 berechnet werden. Hierzu wird Gl. 7 in Gl. 5 eingesetzt. Anschließend wird noch Gl. 6a bzw. 6b eingesetzt.

Der Haken dabei ist, dass die Federsteifigkeit cF unbekannt ist. Hier hilft wohl nur eine experimentelle Bestimmung weiter. Dabei lässt sich auch herausfinden, ob die Federsteifigkeit tatsächlich konstant ist oder nicht. Die Seilkraft Fs entspricht jedoch nicht der Kraft, die auf den Bolzen ausgeübt wird. Die resultierende Kraft F (siehe Skizze 4) auf den Bolzen beträgt laut der nach F umgestellten Gl. 4. Anschließend wird Gl. 8 eingesetzt.

mit:
l: Länge der ungespannten Sehne
cF: Federsteifigkeit
α: Sehnenwinkel
k: Auszuglänge
Wie man sieht, ist die Kraft F nur von drei Parametern (l, cF und α bzw. k) abhängig.
Grundsätzlich gilt: Arbeit ist Kraft mal Weg entlang des Kraftvektors. Ist die Kraft veränderlich (nicht konstant), wie in unserem Fall, muss die Kraft über den Weg integriert werden. Die allgemeine mathematische Formel hierfür zeigt Gleichung 10. Dies ist die kinetische Energie (= Bewegungsenergie), die ein abgeschossener Bolzen hat.

Wie die folgende Skizze (Skizze 5) zeigt, entspricht der Weg der Auszuglänge k. Die Kraft F(x) ist 0 für x = 0 und entspricht Gl. 9 für x = k.

Im linear-elastischen Bereich (Hook'sche Gerade) gilt Gl. 5. Wir berechnen nun die Spannenergie E, d.h. die Arbeit die man aufwenden muss, um die Sehne zu spannen. Dies geschieht ebenfalls nach Gleichung 10, aber diesmal müssen wir mit der Seilkraft Fs und dem Weg s in Seilrichtung rechnen (Gl. 11). Die Spannenergie wird (wenn man Reibungsverluste vernachlässigt) vollständig in kinetische Energie des Bolzens umgewandelt, daher sind die Energien gleich groß.

Wir setzen nun diese Gleichung 11 in Gleichung 10 ein. Da wir cF als linear angenommen haben, können wir den Koeffizienten aus dem Integral rausziehen. Nach Integration erhalten wir die Stammfunktion in den Grenzen s1 (Länge der entspannten Sehne) und s2 (Länge der gespannten Sehne). Dies ist Gleichung 12:

Gl. 12 ist die allgemeine Gleichung. Wir können nun die geometrischen Beziehungen aus unserer Skizze oben einsetzen. s1 (Länge der entspannten Sehne) war l und s2 (Länge der gespannten Sehne) war 2c (doppelte Hypothenuse), siehe Skizze 3.

Nach simplen Umformungen, die hier nicht näher ausgeführt sind, erhalten wir damit die Spannenergie E = 2 cF k2. Hierbei sind die zwei Randbedingungen zu beachten: die Länge der entspannten Sehne beträgt l, d.h. es liegt keine Vorspannung der Sehne vor und cF ist konstant. In diesem Fall ist die Energie proportional zum Quadrat der Auszuglänge k. Gleichung 12 gilt übrigens ganz allgemein, also auch für Bögen. Hierzu ein anschauliches Beispiel: der Bogen der zierlichen Elfe Andariel Blütenstaub hat eine normale Auszuglänge von 70 cm. Nun kommt Karl Kraftprotz, der über einen Kopf größer ist als die Elfe und benutzt ihren Bogen. Da er größer ist und längere Arme hat, zieht er ihren Bogen auf 100 cm aus. Die Auszuglänge beträgt also "nur" 30 cm mehr, das ist nicht ganz das Anderthalbfache (1,43-fache) der vorgegebenen Länge. Die Geschossenergie verdoppelt sich jedoch dabei! Von einem solchen Pfeil getroffen zu werden, macht dann keinen Spaß mehr.
Falls ich irgendwo einen Denk-, Tipp- oder Rechenfehler drinhaben sollte, bitte korrigieren. Geschrieben von Jörg Bolle, 2003. Letzte Änderung am 19.11.2005